令和7年度 春期 応用情報技術者試験 午前 問21
【問題21】
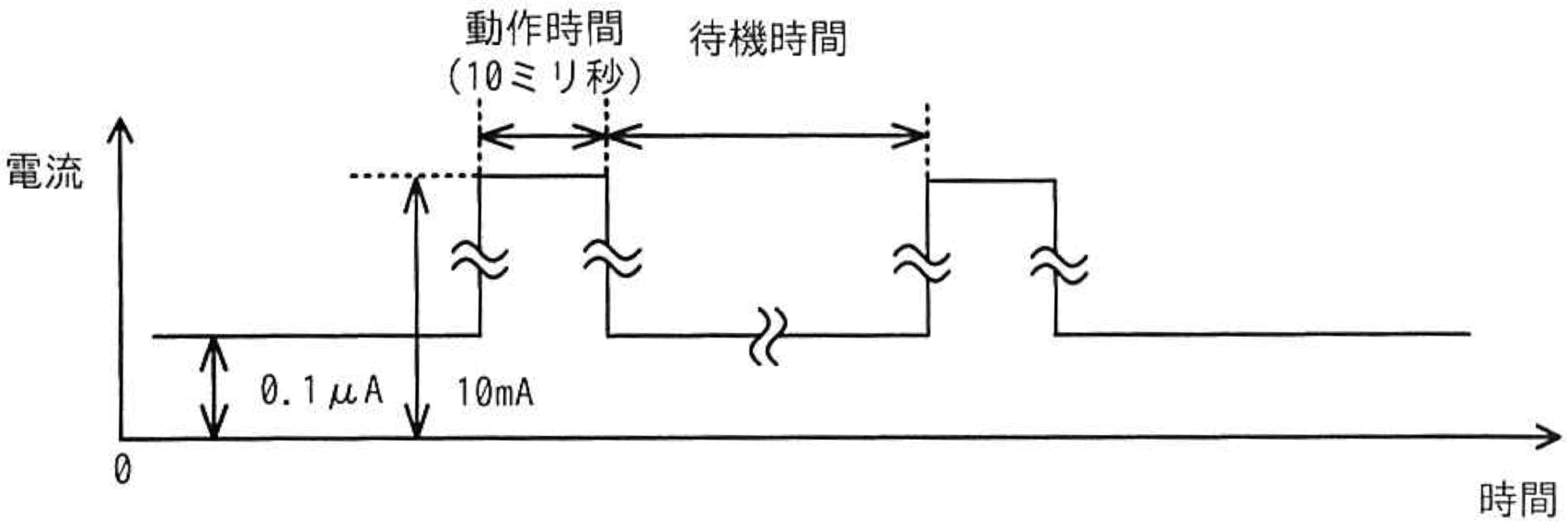
IoTシステムにおいて、センサーの値をゲートウェイに送信するセンサーノードの消費電流を抑えるため、図のような間欠動作を考える。センサーノードの動作時間は10ミリ秒で、その間は平均して10mAの電流が流れる。待機中は常に0.1μAの電流が流れる。間欠動作の平均電流を1μA以下にするための待機時間として、最も短いものはどれか。ここで、平均電流の値を求める時間は十分に長いものとする。
【解説】
求めるべきは、平均電流が1μA以下となる待機時間です。
1回のサイクルの消費電流の合計を考えると、
- 動作時間中の電流量:
10mA × 10ms = 10mA × 0.01秒 = 0.1mAs
- 待機時間を t 秒とすると、待機中の電流量は:
0.1μA × t秒 = 0.1 × 10⁻⁶A × t秒 = 0.1 × 10⁻⁶ × t [As]
1サイクルあたりの総電流量は:
0.1mAs + (0.1 × 10⁻⁶ × t) As
1サイクルあたりの時間は:
(0.01 + t)秒
平均電流は次の式になります:
(0.1 + 0.1×10⁻⁶×t) ÷ (0.01 + t) [A]
これが1μA(= 1×10⁻⁶A)以下になる条件:
(0.1 + 0.1×10⁻⁶×t) ÷ (0.01 + t) ≤ 1×10⁻⁶
両辺に (0.01 + t) を掛けて式を展開:
0.1 + 0.1×10⁻⁶×t ≤ 10⁻⁶×(0.01 + t)
右辺を展開:
0.1 + 0.1×10⁻⁶×t ≤ 10⁻⁸ + 10⁻⁶×t
両辺を整理:
0.1 - 10⁻⁸ ≤ (10⁻⁶ - 0.1×10⁻⁶) × t
0.1 - 10⁻⁸ ≈ 0.1(10⁻⁸は非常に小さいため無視)
(10⁻⁶ - 0.1×10⁻⁶) = 0.9×10⁻⁶
よって:
t ≥ 0.1 ÷ (0.9×10⁻⁶) ≈ 111111
t ≈ 111.1秒
したがって、最も短い待機時間は ウ: 111.1秒 となります。
出典:令和7年度 春期 応用情報技術者試験 午前 問21
